Insane Coloured Triangles 想法
|
相異的兩字母則下一列會得到第三個字母,例如 R 和 G 會得到 B | 相同的兩字母則下一列會得到一樣的,例如 G 和 G 會得到 G |
用這個規則得到第二列是 BGRBR ,然後第三列是 RBGG ,就這樣得到最下面的 B
最初這題我用 Python,相法也很單純把共9種對應全列出來成 dict 然後全丟進去,結果就是 time out
後來想說如果 string 的控制很耗時,那用算的看看吧?把 R G B 三個字對應到三個數字,就想到除以 3 的餘數,恰好三個字的 ASCII 值 52, 47, 42 mod 3 剛好 1, 2, 0,再來要想 0, 1, 2 三數如何運算可以相同得相同,也就是 0#0=0 ,1#1=1 ,2#2=2 ,而相異得第三數,也就是 0#1=2 ,0#2=1 ,1#2=0 。觀察後者得相加後不足 3 的部份即想要的結果,所以用 3 的倍數去扣兩數之和,可以用3或6,其實就是兩數之和再變號,再調整至 0, 1, 2 即可,恰好也滿足前者的要求。
也就是上一列若是 a 和 b,其中 a, b 屬於 { 0 , 1 , 2 },則下一列對應位置是 - ( a + b ),例如 R, G 換成 1, 2 會得對應的數為 - ( 1 + 2 ) = - 3 ,再加 3 或 6 再模 3 得 0,即 B
然而改用數字計算一樣還是 time out,原來字串太長太長了,再來我就想能不能不要透過這樣一層一層的計算,直接從第一列求出最後的結果?
若第一列是兩個字母 a 和 b,則第二列得 - ( a + b )
若第一列是三個字母 a 和 b 和 c ,則第二列是 -(a+b) 、-(b+c),第三列是 - {[-(a+b)]+[-(b+c)]} 得 a + 2b + c
若第一列是四個字母 a 和 b 和 c 和 d,則第二列是 -(a+b)、-(b+c)、-(c+d),第三列是 a+2b+c 、b+2c+d,第四列得 - ( a + 3b + 3c + d )
若第一列是五個字母 a 和 b 和 c 和 d 和 e,則第二列是 -(a+b)、-(b+c)、-(c+d)、-(d+e),第三列是 a+2b+c 、b+2c+d、c+2d+e,第四列得-(a+3b+3c+d)、-(b+3c+3d+e),第五列得 a + 4b + 6c + 4d + e
稍微有頭緒了,最下面的數字會是用最上面的數字乘上巴斯卡三角形得到的係數之和,也就是 C(n,r) ,再由奇偶決定有沒有帶負號。例如六個字母 RGGBBG時,先換成模 3 的數字得 122002,分別乘上C(5,r) , r=0,1,2,3,4,5,得 1*1 + 2*5 + 2*10 + 0*10 + 0*5 + 2*1 = 33 ,變號 -33 再加 3 的倍數再模 3 得 0,即字母 B。
雖然這個結果令人雀躍,但數字很大時也很吃力,若字串長度很可觀,那 C(n,r) 會很巨大似乎不是好辦法,不過倒也不需要真的求出 nCr,其實得 nCr 模 3 的結果也行,反正最後也是要取模。接著去網路上找數論相關的資料,確實有 nCr mod prime number 的討論,但有要求 p > n ,我這個 p = 3 不行,但問題只出在有些 nCr 除以 3 會整除,例如 C(6,2) = 15 同餘 0 (mod 3),是因為 C(6,2) 的計算中出現了約不掉的 3 使他成為 3 的倍數,那麼我就在求 nCr 的過程中檢查分母分子 3 的個數,最後就解決了這個問題,剩下就是小細節像是 nCr 有對稱性(餘組合定理)可以減少一些計算,最後是用 Java 完成了這個 Kata,原本 16 秒內的要求壓在 8 秒多完成,非常有成就感。
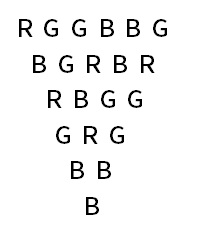


留言
張貼留言