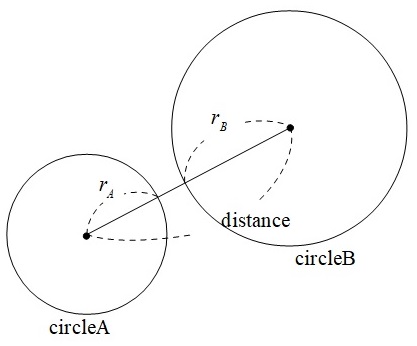
矩形與矩形碰撞(皆旋轉矩形)

碰撞主題的最後,是凸多邊形碰撞的解法應用在矩形上,想法來自 Stack Overflow : How to check intersection between 2 rotated rectangles? 的回應 ,正如標題描述要處理的是,兩個有旋轉的矩形之碰撞檢定。 以四邊形 ABCD 和三角形 EFG 為例,上圖是邊界有相交,下圖是沒有,當兩凸多邊形未碰撞時,中間會有空隙一定找的到一條直線 L 使得兩個圖形各在直線的異側,如下圖: 顯然這樣的直線不是唯一,不只可以將直線平移,其至稍微旋轉一點也可以,在兩凸多邊形邊界未相交時,可以隔開兩個圖形的直線有無限多條,如下圖有 L、M、N 三條: 換句話說只要找出一條直線,可使得兩個圖形各落在直線的一側,就確定兩圖形沒有碰撞,那麼這樣的直線怎麼找呢?再觀察上圖,顯然隔開的直線可以取「平行多邊形的一邊的直線」,例如上圖的直線 L 就平行線段 FG,而直線 M 和直線 N 就平行線段 AB,其實也不是一定要平行多邊形的邊,例如上圖中斜率介於 L 和 M 之間的直線也能夠將兩圖形分開,只是我們從平行多邊形一邊的直線來著手。 再回來看四邊形 ABCD 在左邊,三角形 EFG 在右邊,被直線 L 隔開的圖: 如果兩凸多邊形被直線 L 分開,應該有什麼性質呢?我們考慮將兩個圖形沿著直線 L 的方向投影出去,也就是取和直線 L 垂直的直線 N ,將四邊形 ABCD 與三角形 EFG 都投影到直線 N 上,各自會得到線段,如下圖: 顯然投影的兩個線段不會相交,四邊形 ABCD 在直線 N 上的正射影是線段 A'C',而三角形 EFG 在直線 N 上的正射影是線段 F'G',兩個線段並沒有重疊,上圖是取「平行線段 CD 的直線 L 和垂直的直線 N」,如果看另外一組: 上圖是取「平行線段 EG 的直線 L 和垂直的直線 N」,同樣的將四邊形 ABCD 和三角形 EFG 投影到直線 N 上的結果,顯然洋紅色與青綠色兩個投影線段這次就有重疊了,兩個多邊形在「邊 EG 的法向量」上的正射影有重疊,表示我們無法用平行 EG 的直線將兩個圖形分開在兩邊,但這不代表兩個圖形就有碰撞,只是代表不能用平行線段 EG 的直線去隔開兩個圖形。可能用別的邊和法向量看投影,就可...