矩形與矩形碰撞(皆旋轉矩形)
碰撞主題的最後,是凸多邊形碰撞的解法應用在矩形上,想法來自 Stack Overflow : How to check intersection between 2 rotated rectangles? 的回應,正如標題描述要處理的是,兩個有旋轉的矩形之碰撞檢定。
以四邊形 ABCD 和三角形 EFG 為例,上圖是邊界有相交,下圖是沒有,當兩凸多邊形未碰撞時,中間會有空隙一定找的到一條直線 L 使得兩個圖形各在直線的異側,如下圖:
顯然這樣的直線不是唯一,不只可以將直線平移,其至稍微旋轉一點也可以,在兩凸多邊形邊界未相交時,可以隔開兩個圖形的直線有無限多條,如下圖有 L、M、N 三條:
換句話說只要找出一條直線,可使得兩個圖形各落在直線的一側,就確定兩圖形沒有碰撞,那麼這樣的直線怎麼找呢?再觀察上圖,顯然隔開的直線可以取「平行多邊形的一邊的直線」,例如上圖的直線 L 就平行線段 FG,而直線 M 和直線 N 就平行線段 AB,其實也不是一定要平行多邊形的邊,例如上圖中斜率介於 L 和 M 之間的直線也能夠將兩圖形分開,只是我們從平行多邊形一邊的直線來著手。
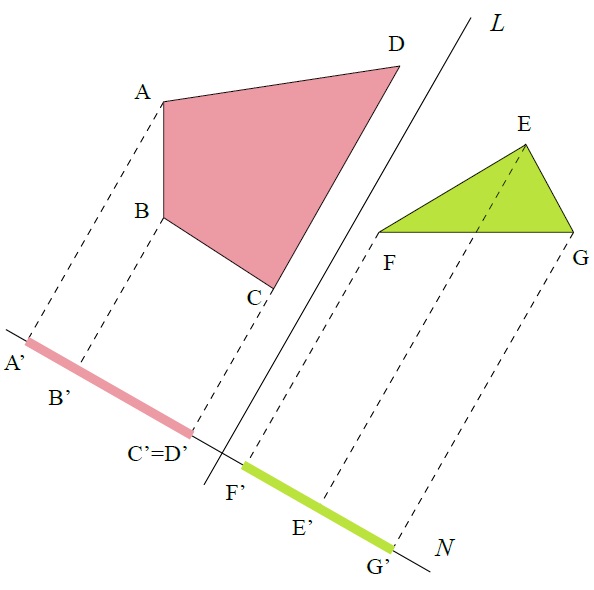
再回來看四邊形 ABCD 在左邊,三角形 EFG 在右邊,被直線 L 隔開的圖:
如果兩凸多邊形被直線 L 分開,應該有什麼性質呢?我們考慮將兩個圖形沿著直線 L 的方向投影出去,也就是取和直線 L 垂直的直線 N ,將四邊形 ABCD 與三角形 EFG 都投影到直線 N 上,各自會得到線段,如下圖:
顯然投影的兩個線段不會相交,四邊形 ABCD 在直線 N 上的正射影是線段 A'C',而三角形 EFG 在直線 N 上的正射影是線段 F'G',兩個線段並沒有重疊,上圖是取「平行線段 CD 的直線 L 和垂直的直線 N」,如果看另外一組:
上圖是取「平行線段 EG 的直線 L 和垂直的直線 N」,同樣的將四邊形 ABCD 和三角形 EFG 投影到直線 N 上的結果,顯然洋紅色與青綠色兩個投影線段這次就有重疊了,兩個多邊形在「邊 EG 的法向量」上的正射影有重疊,表示我們無法用平行 EG 的直線將兩個圖形分開在兩邊,但這不代表兩個圖形就有碰撞,只是代表不能用平行線段 EG 的直線去隔開兩個圖形。可能用別的邊和法向量看投影,就可以隔開了
但是投影要怎麼判斷?若我們在直線 N 上取一個 P 點,如下圖,觀察從 P 點連出去每個投影點的向量之結果:
由於這些投影點在直線 N 上呈現一個序列,要判斷多邊形在直線上的投影線段是否相交,可看點的前後關係,如上圖四邊形 ABCD 的投影之中最右的點 C',在三角形的投影之中最左的點 F' 的左邊,這就保證兩個投影線段不會相交,我們可用向量 PA'、向量 PB'、.... ... 向量 PE'、向量 PG' 來比較,因為同方向且同始點的關係,向量的大小可決定終點的落點前後之順序,而這個大小關係又可用向量內積來看,也就是向量 PA內積向量 N 、向量 PB 內積向量 N 、... ... 、向量 PF 內積向量 N、向量 PG 內積向量 N,這和 P 點是取在直線 N 上的何處並沒有關係,就算取直線 L 與直線 N 的交點,使得內積值可能為負數,一樣也可以從大小來判斷是否完全偏向一邊。
甚至取不是直線 N 上的 P 點也可以,以下圖為例:
要計算向量 PC 內積向量 N 的內積值,若取另外的 O 點,則 PC·N = ( OC - OP )·N = OC·N - OP·N ,其中 OP·N 是定值,並不會影響這些大小順序的比較,而為了方便計算,我們取 O 為原點 (0, 0),換句話說直接拿多邊形的頂點 A, B, C, ... F, G 的坐標值來和法向量內積即可。
所以這裡的邏輯是這樣:
- 對一個邊求出法向量,利用向量 (a, b) 則有 (b, -a)與之垂直
- 將每個頂點和前面求出的法向量內積
- 得一連串的內積值,將四邊形得到的四個內積值找出最大與最小,三角形得到的三個內積值也找出最大與最小
- 比較是否四邊形的最大仍然比三角形的最小還小,或是四邊形的最小仍然比三角形的最大還大
- 是的話就存在分割直線,兩多邊形不相交
- 否的話再回到第一步,換下一個邊找法向量
- 若所有邊都試過,投影都會重疊,表示兩多邊形碰撞
有了這個先備知識,就能來處理本來的問題:檢定兩個旋轉矩形是否碰撞。而且因為矩形的特性:鄰邊垂直,還有四個邊只有兩種斜率,我在檢定的過程減少一些計算,使用這個方法的前提是必須有矩形的四個頂點坐標(旋轉後的坐標),存放在 pointsA 和 pointsB 兩個 Point[] 陣列中,Point 是 Java.awt.Point 內有 .x .y 可存放點。
參考 Java Code :
public boolean isRectRotateRectCollide(Rectangle rectA, Rectangle rectB) {
Point[] pointsA = new Point[4];
Point[] pointsB = new Point[4];
int thetaA = rectA.getRotateAngle(), thetaB = rectB.getRotateAngle();
Point centerA = rectA.center, centerB = rectB.center;
for(int i=0; i<4; i++) {
pointsA[i] = rotate(rectA.rectParticle[i], centerA, thetaA);
pointsB[i] = rotate(rectB.rectParticle[i], centerB, thetaB);
} // Rectangle.rectParticle 是我設計物件擺正矩形的四個頂點陣列
// rotate 方法是將 Point 依中心旋轉得新的 Point
for(int i=0; i<2; i++) { // 因為矩形邊斜率只有兩種:P0P1和P1P2
int normalX = pointsA[i+1].y - pointsA[i].y; // 法向量x
int normalY = pointsA[i].x - pointsA[i+1].x; // 法向量y
int projectedA, projectedB;
int minA = Integer.MAX_VALUE, maxA = Integer.MIN_VALUE;
int minB = Integer.MAX_VALUE, maxB = Integer.MIN_VALUE;
for(int k=0; k<4; k++) { // 走訪四個、四個頂點
if(k==i || k==i+2) { // 對 rectA 來說只需要判斷其中兩個內積值
projectedA = pointsA[k].x * normalX + pointsA[k].y * normalY; // 和邊法向量內積
minA = Math.min(minA, projectedA);
maxA = Math.max(maxA, projectedA);
}
projectedB = pointsB[k].x * normalX + pointsB[k].y * normalY; // rectB 四個內積值都要
minB = Math.min(minB, projectedB);
maxB = Math.max(maxB, projectedB);
}
if(maxA < minB || minA > maxB) { // 比較內積最大最小值來判斷投影是否隔開
return false;
}
} // 以上是矩形 rectA 的邊是否存在分隔的直線
for(int i=0; i<2; i++) { // 以下是矩形 rectB 的邊是否存在分隔的直線
int normalX = pointsB[i+1].y - pointsB[i].y;
int normalY = pointsB[i].x - pointsB[i+1].x;
int projectedA, projectedB;
int minA = Integer.MAX_VALUE, maxA = Integer.MIN_VALUE;
int minB = Integer.MAX_VALUE, maxB = Integer.MIN_VALUE;
for(int k=0; k<4; k++) {
projectedA = pointsA[k].x * normalX + pointsA[k].y * normalY;
minA = Math.min(minA, projectedA);
maxA = Math.max(maxA, projectedA);
if(k==i||k==i+2) { // 對 rectB 來說只需要判斷其中兩個內積值
projectedB = pointsB[k].x * normalX + pointsB[k].y * normalY;
minB = Math.min(minB, projectedB);
maxB = Math.max(maxB, projectedB);
}
}
if(maxA < minB || minA > maxB) {
return false;
}
}
return true;
}






留言
張貼留言